Here we describe the uncertainty in the algorithms used to estimate surface and cloud properties from satellite data with the Cloud and Surface Parameter Retrieval (CASPR) system for polar AVHRR. Validation is an ongoing process, the primary problem being the scarcity of in situ observations in the polar regions.To date, studies have been done primarily with surface and aircraft data collected during the yearlong Surface Heat Budget of the Arctic Ocean (SHEBA) experiment (Moritz et al., 1993).Additionally, surface radiation fluxes have been compared to measurements made at two Antarctic locations. See Key (2002) for algorithm details.
Estimates of algorithm uncertainty obtained by comparing satellite-derived quantities with surface observations are comprised of instrument noise (satellite and surface-based), instrument calibration errors, differences in how the geophysical parameter is observed (e.g., a satellite area observation versus a point measurement as well as temporal differences), and algorithm inaccuracies (biases in radiative transfer models, incorrect assumptions, unmodeled physics, etc.). If we assume instrument noise to be random, then averaging many observations reduces the uncertainty by an amount proportional to the square root of the number of observations.So when averaging over space and time, instrument noise is a negligible source of uncertainty.
The other three errors sources tend to manifest themselves as biases, with variability around the bias resulting from variability in the parameter being observed.For example, thermal channel calibration may produce radiances that are consistently high or low, cloud amount may be overestimated because pixels are often partially cloudy but assumed to be fully cloudy or clear, or simulated radiances from a radiative transfer model may be biased because cloud scattering is incorrectly parameterized.In these cases the retrievals of surface and cloud properties may be biased high or low. In reality, the retrieval error will not simply be a bias, but will vary around the bias. Variability will be introduced if calibration errors, algorithm inaccuracies, or observation system differences are not the same for all conditions.For example, if certain types of clouds are more difficult to detect than others, or if the thermal channel calibration is less accurate for low temperatures than high temperatures, then the error in clear sky surface temperature estimates will be small for some conditions and larger for others. As with instrument noise, averaging over many observations will reduce the uncertainty.If the variability is not random, the bias will be affected.
How do algorithm uncertainties affect the significance of long-term trends in AVHRR retrievals? Systematic biases will have no significant impact because they simply shift the trend line up or down (higher or lower values of the estimated parameter) but do not change its slope. If the uncertainties are larger than the trends, then the trends may not be valid.This may be the case for instantaneous observations, but will not be the case for trends based on averages over time or space, which will have small relative uncertainties in the estimated parameters.Care must be taken, of course, to ensure that there are no trends in the error sources. If, for example, the sensor response changes systematically over time, or if a cloud detection algorithm performs poorly for cirrus clouds and cirrus amount exhibits a trend over time, then artificial trends in parameter retrievals may be introduced.
Algorithm Uncertainties
In this section algorithm biases and uncertainties (root-mean-square differences) are estimated through comparisons of satellite retrievals and in situ measurements.
Comparisons with SHEBA surface observations were done by inverting measurements of the upwelling longwave flux to obtain temperature.Details are given in Key et al. (1997).An example of the comparison is shown in Figure 1. Results over all-sky conditions (i.e., clear and cloudy) yielded a bias (mean error) of –1.6 K and a root-mean-square-error (RMSE) of 6 K for the all-sky surface temperature.A negative bias indicates that the satellite retrieval is less than the surface observation. Comparisons to three International Arctic Buoy Program (IABP) buoys located from approximately 20 km to 450 km from the SHEBA icebreaker Des Groseilliers in April-July 1998 show that the AVHRR temperatures track the buoy temperatures quite well, with mean monthly differences typically less than 2 K. >Retrievals for clear sky conditions have much smaller uncertainties than for all-sky conditions, on the order of -0.3 K for the bias and 1-2 K for the RMSE (Key et al., 1994).
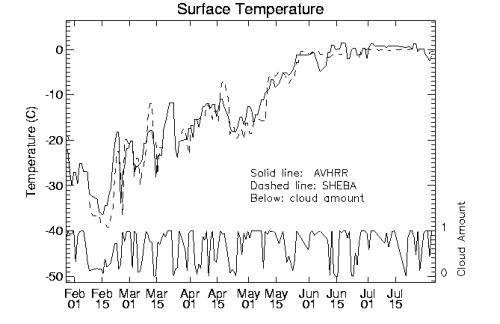
Figure 1. Comparison of satellite-derived and surface measurements of the surface skin temperature during SHEBA.Cloud amount is also shown.
Measurements of the upwelling and downwelling shortwave flux measured at the SHEBA camp were used to compute an all-sky albedo. Satellite-derived and surface measurements are shown in Figure 2.This comparison yields a bias of –0.028 and a RMSE of 0.08 for the all-sky surface albedo. Retrievals for clear sky conditions have smaller uncertainties than for all-sky conditions.
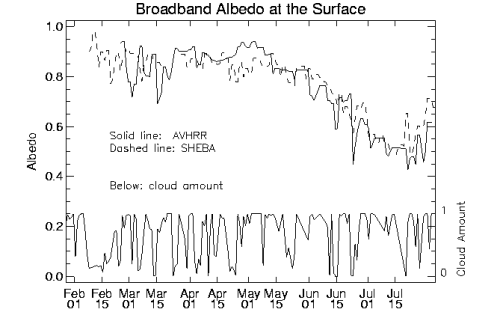
Figure 2. Comparison of satellite-derived and surface measurements of the surface broadband albedo during SHEBA.Cloud amount is also shown.
Cloud amount at the SHEBA camp is based on three-hourly synoptic observations (human observer). Comparisons with satellite-derived cloud amount for 25 x 25 km area centered on the SHEBA ship (not shown) from September 1997 through August 1998 yield a bias of 0.1 and a RMSE of 0.3. Additional details are given in Key et al. (2001).
The Depolarization and Backscatter Unattended Lidar (DABUL)
instrument was deployed as part of SHEBA. Small raindrops,
water cloud droplets, and fog are considered spherical and have depolarization
ratios that theoretically approach 0. Non-spherical particles such as ice crystals and snowflakes contain a
cross-polarized component produced by internal reflections and refractions and
can exhibit depolarization ratios greater than 0.30. By data point inspection and comparisons with the microwave radiometer
liquid water column measurements, it was determined that DABUL depolarization
values of less than 0.11 indicate liquid water phase.
Figure 3 gives a comparison of AVHRR-derived cloud phase and lidar depolarization ratio during the SHEBA year. The lidar results are for the highest altitude layer detected.Multilayer, multiphase cases were excluded from the analysis.The AVHRR results are for a 50 x 50 km area around the lidar location were used, but only for scenes with a cloud fraction of at least 0.6 (60%). The AVHRR phase labeling is zero for water and one for ice; intermediate values correspond to scenes with both phases present in varying proportions.The figure illustrates that for homogeneous scenes there is almost perfect agreement between the lidar and satellite determinations of phase; i.e., all cases labelled as water (ice) cloud by the AVHRR algorithms, day or night, are also labelled as water (ice) cloud by the lidar method. For the cases where the AVHRR algorithm found both phases present but more water than ice cloud - as indicated by an area average phase value less than 0.5 - the lidar cloud type was usually water. The results for the cases with more ice than water cloud show a similar pattern.Overall the satellite retrievals of cloud particle phase have an accuracy of approximately 95% (Key and Intrieri, 2000).
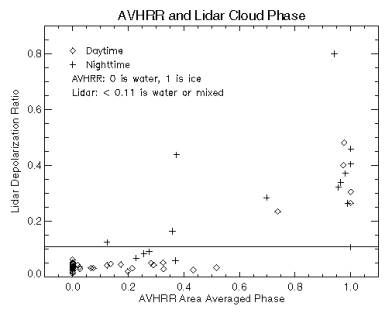
Figure 3. Cloud particle phase from the AVHRR and lidar depolarization ratio during the SHEBA year. Depolarization ratios less than 0.11 are primarily water or mixed-phase clouds.The AVHRR results use a value of zero for water and one for ice; intermediate values correspond to scenes with both phases present.
Cloud optical depth and particle size retrievals have not been examined in detail due to the lack of in situ measurements. Some comparisons have been done with aircraft observations during SHEBA, particularly with the Canadian National Research Council (NRC) Convair.The effective radius for water (liquid) clouds from the AVHRR were comparable to those measured by the Convair, typically within 1-2 μm for clouds with effective radii in the 8-10 μm range.For ice clouds the differences are larger, on the order of 10 μm for particles with effective “radii” in the range of 30-100 μm (Gultepe et al., 2003). Figure 4 provides one example from SHEBA.
Cloud top pressure is currently being validated with SHEBA lidar and radar measurements.Figure 5 shows the monthly mean cloud top pressure estimated with data from the TIROS Operational Vertical Sounder (TOVS), the AVHRR, and surface-based lidar. The two satellite estimates are similar even though the retrieval methods are very different. The lidar estimate is considerably higher (estimated cloud top is at a lower altitude) during the summer, most likely because summertime clouds tend to be thicker on average, and the lidar cannot penetrate to the tops of clouds with optical thicknesses larger than approximately 3. It is difficult to provide an uncertainty with this limited comparison, but a value of 50-75 mb is probably reasonable.
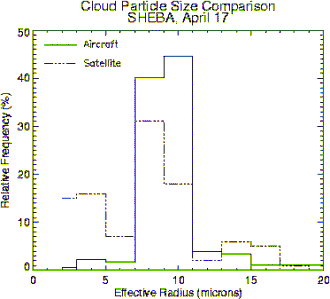
Figure 4. Relative frequency distribution of satellite-derived and aircraft measurements of liquid cloud particle effective radius for one case study from SHEBA.
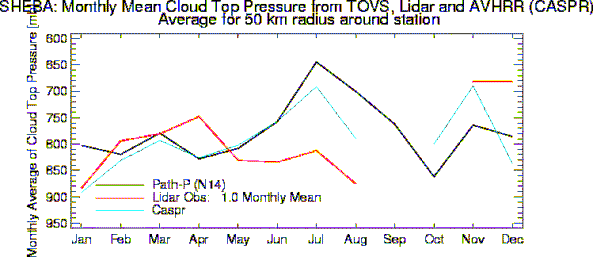
Figure 5. Monthly mean cloud top pressure from TOVS, AVHRR, and lidar during SHEBA.
Radiative fluxes are calculated with the neural network procedure called FluxNet.Root mean square differences between the neural network and the radiative transfer model for downwelling shortwave and longwave fluxes at the surface are on the order of 2-3% with biases near zero. Comparisons of instantaneous satellite-derived surface fluxes with SHEBA surface measurements yield a bias of 9.8 W m-2 and an RMSE of 34.4 W m-2 for downwelling shortwave radiation. For the downwelling longwave flux the bias and RMSE are 2.1 and 22.4 W m-2, respectively. Figure 6 shows the results for SHEBA.
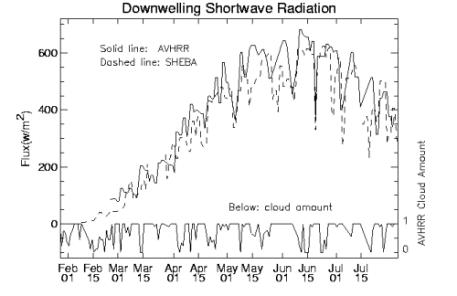
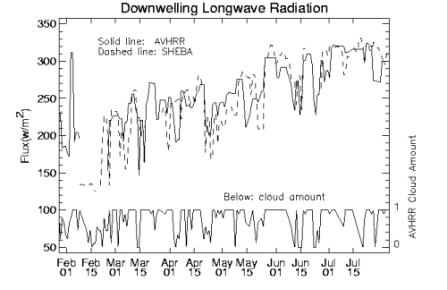
Figure 6. Comparison of satellite-derived and surface measurements of the downwelling shortwave flux at the surface (top) and the downwelling longwave flux at the surface (bottom).Cloud amount is also shown.
Comparisons of monthly mean values with measurements at Neumayer Station, Antarctica show differences of less than 10 W m-2 for the net shortwave flux and less than 8 W m-2 for the net longwave flux.For South Pole Station the longwave results are similar but the shortwave differences are somewhat higher.Figure 7 shows the results for Neumayer Station.See Pavolonis and Key (2003) for more information.
Key et al. (1997) address the combined uncertainties in satellite estimates of the surface radiation fluxes from a statistical perspective.The propagation of errors in the individual surface and cloud property retrievals is assessed as a function of the individual errors and the sensitivity of surface fluxes to changes in each variable.The method produced uncertainties in the range of 30-40 W m-2 for the downwelling shortwave flux, 9-15 W m-2 for the downwelling longwave flux, and 20-30 W m-2 for the net flux.
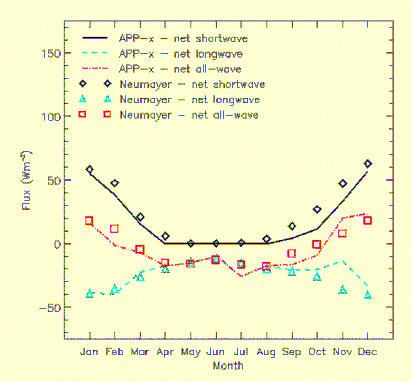
Figure 7. Comparison of monthly mean satellite-derived (APP-x) and surface measurements of the net radiative fluxes at Neumayer Station, Antarctic.
Some algorithms use different spectral channels in the presence/absence of sunlight.Cloud detection, optical depth, effective radius, and particle phase all take advantage of reflective channels during the day.How consistent are the results for daytime and nighttime retrievals? Because these algorithms all use the AVHRR 3.7 μm channel in both day and night retrievals, a portion of the spectrum that includes both emitted thermal and reflected solar radiation, it is not possible to test the day-night differences simultaneously. Instead we provide the validation information detailed in the previous sections, and a few illustrations of retrievals for images that were part dark and part sunlit.Such comparisons are, of course, qualitative.Figure 8 shows retrievals for the cloud mask, cloud optical depth, particle effective radius, and particle phase for one winter day over the Arctic. The lower latitudes are sunlit; the area above approximately 80 degrees latitude is dark. There are no obvious day-night dependencies in the retrieval results.
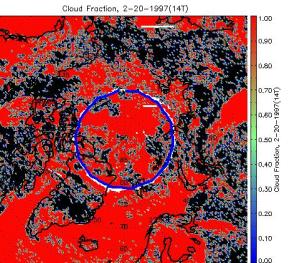
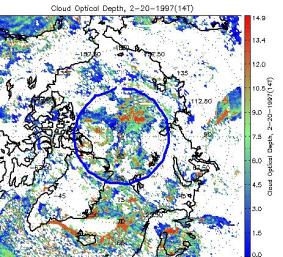
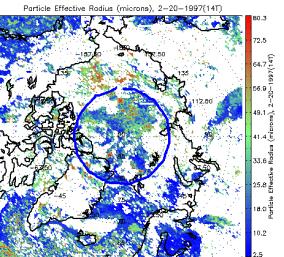
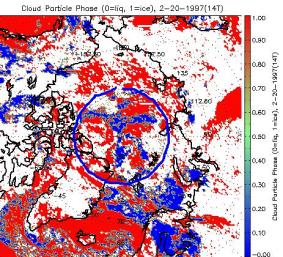
Figure 8. Retrievals for the cloud mask (upper left), visible cloud optical depth (upper right), particle effective radius (lower left), and particle phase (lower right) for one winter day over the Arctic.The lower latitudes are sunlit; the area above approximately 80 degrees latitude is dark, as denoted by the blue circle.
Personnel
This research is being (or was) performed by the following people: Jeff Key and Xuanji Wang.
Gultepe, I., G. Isaac, J. Key, T. Uttal, J. Intrieri, D. Starr, and K. Strawbridge, 2002, Dynamical and Microphysical Characteristics of Arctic Clouds Using Integrated Observations Collected Over SHEBA During the April 1998 FIRE-ACE Flights of the Canadian Convair, Meteorol. Atmos. Physics, accepted.
Key, J., 2002, The cloud and surface parameter retrieval (CASPR) system for polar AVHRR, Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin, Madison, 59 pp.
Key, J., X. Wang, J. Stroeve, and C. Fowler, 2001, Estimating the cloudy-sky albedo of sea ice and snow from space. J. Geophys. Res., 106(D12), 12,489-12497.
Key, J. and J. Intrieri, 2000, Cloud particle phase determination with the AVHRR, J. Appl. Meteorol., 39(10), 1797-1805.
Key, J., A.J. Schweiger, and R.S. Stone, 1997, Expected uncertainty in satellite-derived estimates of the high-latitude surface radiation budget, J. Geophys. Res., 102(C7), 15837-15847.
Key, J., J. Collins, C. Fowler, and R. Stone, 1997, High-latitude surface temperature estimates from thermal satellite data, Remote Sensing Environ., 61, 302-309.
Key, J., J.A. Maslanik, T. Papakyriakou, M.C. Serreze, and A.J. Schweiger, 1994, On the validation of satellite-derived sea ice surface temperature, Arctic, 47(3), 280-287.
Moritz, R.E., J.A. Curry, N. Untersteiner, and A.S. Thorndike, 1993: Prospectus: Surface heat budget of the Arctic Ocean. NFSF-ARCSS OAII Tech. Rep. 3, 33 pp. Available from the SHEBA Project Office, Polar Science Center, Applied Physics Laboratory, University of Washington, Seattle, WA 98105.
Pavolonis, M. and J. Key, 2003, Antarctic cloud radiative forcing at the surface estimated from the AVHRR Polar Pathfinder and ISCCP D1 data sets, 1985-1993, J. Appl. Meteorol., accepted. Available on-line at http://stratus.ssec.wisc.edu /papers/Antarctic_cldforce.pdf.